目的：estimation and correction for eddy current induced distortion, subject movement. susceptibility field can also be included.

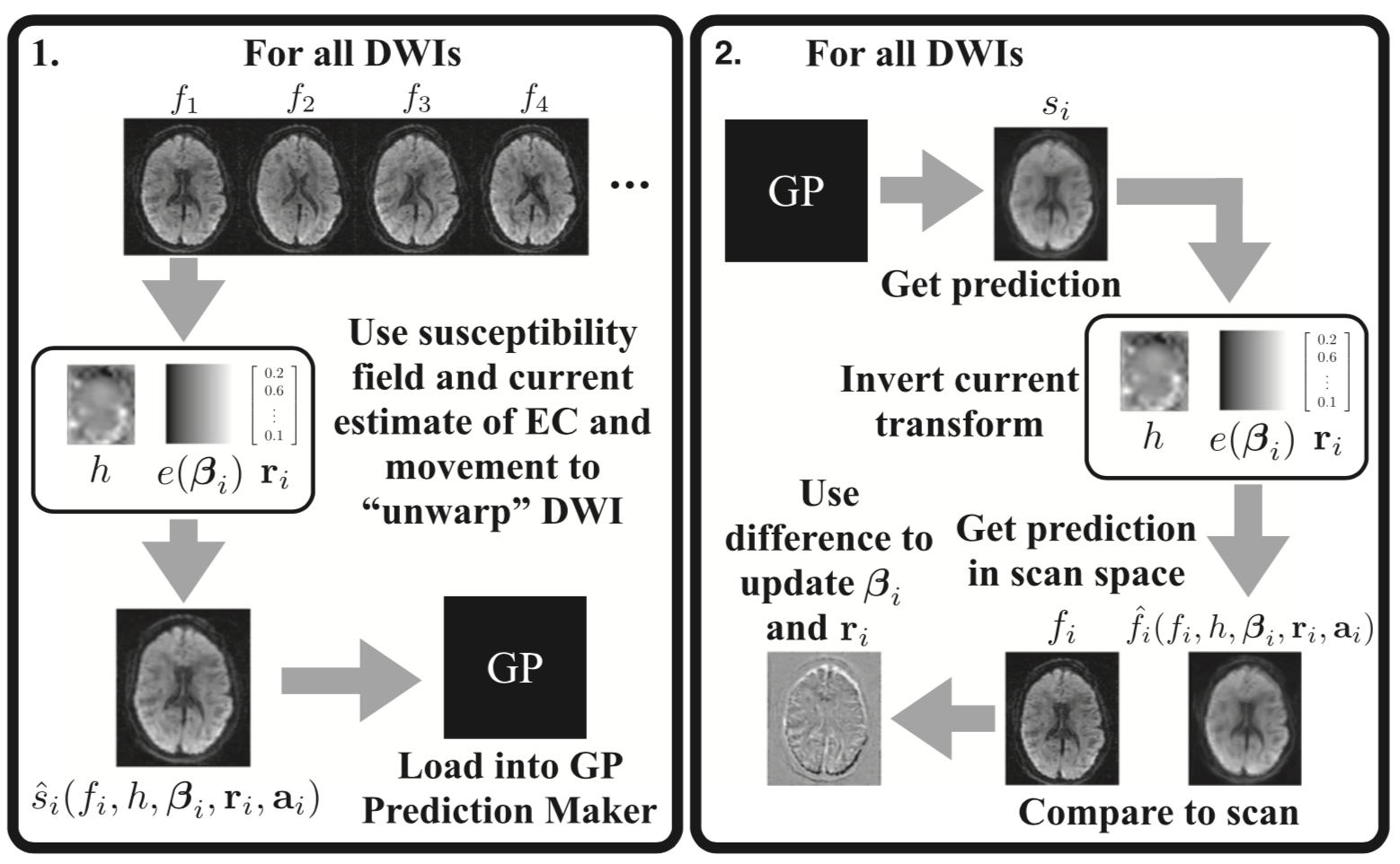
  • register each volume to a model free prediction of what each volume should look like
    • common assumption in registration: images are identical except for geometric transform
    • in dMRI, images with different gradient weighting have different contrast
  • linear (combination of gradients) EC-model is insufficient for high resolution data → higher order model better

Including susceptibility-induced field

通过dual echo-time fieldmap sequence或者reverse gradient method

一般用TOPUP产生的susceptibility map

EC-induced distortion: in plane shears/ zooms/ translations along PE direction。Low order polynomial of gradient field.

Combining the fields

EC-induced field : 在MRI坐标系下静止

susceptibility induced field：相对人体坐标系静止

$\mathbf{x’=R_i^{-1}x+d_x}[h+w(e(\beta_i),\mathbf{r_i}),\mathbf{a_i}]$

$\mathbf{x}$表示reference space $s$ (susceptibility field $h$ is estimated in reference space)中的坐标，$\mathbf{x’}$是observed space $f$ 中的坐标。

坐标逆变换

$\mathbf{x’=R_i(x+d_x}[h+w(e(\beta_i),\mathbf{r_i}),\mathbf{a_i}]^{-1})$

$d_x[h+w(e(\beta_i),\mathbf{r_i}),\mathbf{a_i}]^{-1}$是$d[h+w(e(\beta_i),\mathbf{r_i}),\mathbf{a_i}]$整个空间的displacement field矩阵求逆后坐标 $\mathbf{x}$ 处的值。如果图像不是方的，也就是矩阵宽高不等怎么求逆？

Resampling the images

因为变换后的坐标$\mathbf{x’}$不一定是整数，所以需要插值重采样。同时仿照我们在多重积分坐标变换中做的，再乘上雅各比矩阵，否则变换后的坐标疏密不均。

$\hat{s_i}(\mathbf{x};f_i,h,\mathbf{\beta_i,r_i,a_i})=f_i(\mathbf{x’})J_x(h,\mathbf{\beta_i,r_i,a_i})$

逆变换

$\hat{f_i}(\mathbf{x};s_i,h,\mathbf{\beta_i,r_i,a_i})=s_i(\mathbf{x’})J_x^{-1}(h,\mathbf{\beta_i,r_i,a_i})$

Predicting diffusion data

因为不同的gradient获得的dMRI图像对比度都是不同的，因此不能简单的将所有gradient下的图像register到某一个图像上。

本文中是用GP，根据其他所有gradient下的图像，预测一个gradient下的图像应该长什么样，然后将当前gradient下的图像配准到预测的图像上。

不懂为什么配准就可以去除eddy，susceptibility的影响？前面的combine the fields有什么用？

The registration algorithm

初始化$\beta_i,r_i$为0

for M iterations:

计算$\hat{s_i}(\mathbf{x};f_i,h,\mathbf{\beta_i,r_i,a_i})$，$i\in [1,N]$

训练GP model

从GP model 预测$s_i$

逆变换回$\hat{f_i}(\mathbf{x};s_i,h,\mathbf{\beta_i,r_i,a_i})$

用$f_i-\hat{f_i}$更新$\beta_i,r_i$

\[D\left(\begin{bmatrix}\beta_i^{k+1}\\r_i^{k+1}\end{bmatrix}-\begin{bmatrix}\beta_i^{k}\\r_i^{k}\end{bmatrix}\right)=\hat{f_i}-f_i\] \[D=\left[\frac{\partial \hat{f_i}}{\partial \beta_{1i}}\cdots\frac{\partial \hat{f_i}}{\partial \beta_{ni}};\quad \frac{\partial \hat{f_i}}{\partial r_{1i}}\cdots\frac{\partial \hat{f_i}}{\partial r_{mi}}\right]\]

梯度下降方法 $D=\nabla f_i$

Data requirements for eddy

  • 相反的梯度方向。$-\mathbf{g,g}$，diffusion 的信息相同，distortion的信息差距大
  • 不同的采集方式，比如相反的PE-direction。

Second level modeling

eddy has no inherent knowledge of the “undistort- ed space” and just registers all volumes towards an average space. If the diffusion gradients are evenly distributed on the whole sphere, that space will be close to “undistorted space”

model the EC-estimates as a function of the diffusion gradients with zero intercept，为什么这个second level model 可行？

Final resampling