Deep-Learning Methods for Parallel Magnetic Resonance Image Reconstruction

image domain: SENSE

k-space: SMASH (simultaneous acquisition of spatial harmonics), GRAPPA (generalized auto- calibrating partial parallel acquisition)

Classical parallel imaging in the image space

noise amplification: g-factor

iterative methods to reduce computing & memory requirements

(gradient descent, Landweber iterations, conjugate gradient)

acceleration factor $\ll$ coil number

Nonlinear regularization & Compressed sensing

1. compressed sensing (wavelet transform ) + pseudorandom sampling

2. TV, TGV regularization(Fourier domain ) + radial/ spiral sampling

   primal-dual method，TGV (Second Order Total Generalized Variation (TGV) for MRI)

3. low rank based regularization

Image Quality assessment: $\checkmark$ NRMSE, SSIM, PSNR 与gold standard 对比的方法

                                          $$$\times$  SNR based metrics

Classical parallel imaging in the k-space

Linear k-space interpolation in GRAPPA

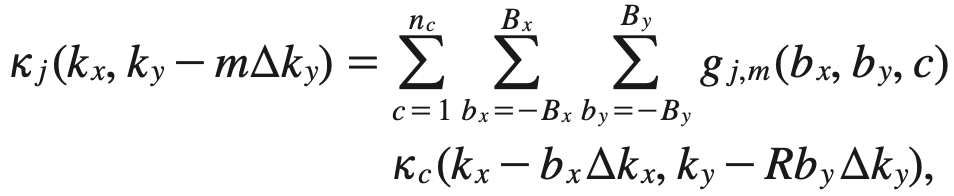
第 j 个线圈的没采集的 k-space 数据 可以由 附近位置，其他所有coil采集的k-space data linear combination 获得

$g_{j,m}()$是权重系数，可以通过采集reference scan或者ACS获得。

原理？why the convolution kernel is shift-invariant

Advantage: Lower g-factor, smooth g-factor map than SENSE

disadvantage: noise amplification

Advances in k-space interpolation methods

To reduce noise

iterative SPIRiT: enforcing self-consistency among the k-space data in multiple receiver coils by exploiting the correlations between neighbor- ing k-space points

(NL)-GRAPPA: nonlinear k-space interpolation for estimating missing k-space points for uni- formly undersampled parallel imaging acquisitions

Low rank matrix completion for k-space reconstruction

Machine-learning methods for parallel imaging in the image space

iterative algorithm → structure of neural network; every layer → iteration step?

Machine-learning methods for parallel imaging in the k-space

1. scan-specific ACS lines to train neural networks (like GRAPPA, NL-GRAPPA)

   1. robust artificial neural network for k-space interpolation (RAKI)

      Scan‐specific robust artificial‐neural‐networks for k‐space interpolation (RAKI) reconstruction: Database‐free deep learning for fast imaging

      use CNNs to train, using ACS data with MSE loss

      reduce noise using coil geometry not image structure

      disadvantage: computational burden, training for each scan

      residual RAKI: residual CNN to reduce noise & remove artifacts

      Accelerated MRI using residual RAKI: Scan-specific learning of reconstruction artifacts

      Accelerated simultaneous multi-slice MRI using subject-specific convolutional neural networks

2. using training databases to train

   Deep SPIRiT:

   DeepSPIRiT: Generalized parallel imaging using deep convolutional neural networks

   normalize training data using Coil compression

   Array compression for MRI with large coil arrays

   Hankel-matrix based