Deep MRI Reconstruction Unrolled Optimization Algorithms Meet Neural Networks
Three categories: data driven [6-16], model driven [23-26], integrated [17-22]
Basics of deep learning and MRI reconstruction
Compressed sensing: sparsity prior is enforced by sparsifying transform or data-driven dictionaries. (Cons: high computational complexity)
deep learning: goes beyond CS by extending key ingredients of CS, adaptive sparsity and non-linearity of the representation
Model-driven deep learning for fast MR
establish the model → choose optimization algorithm → unroll the algorithm to deep network
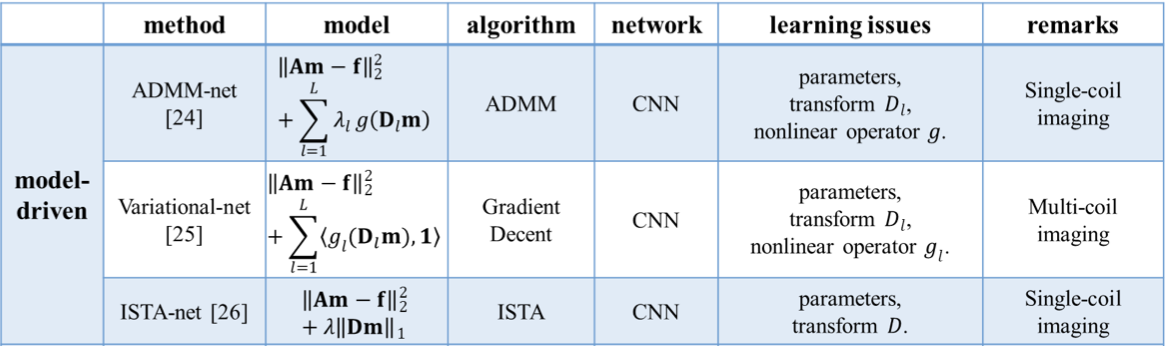
1) ADMM-net (alternating direction method of multipliers) (single coil)
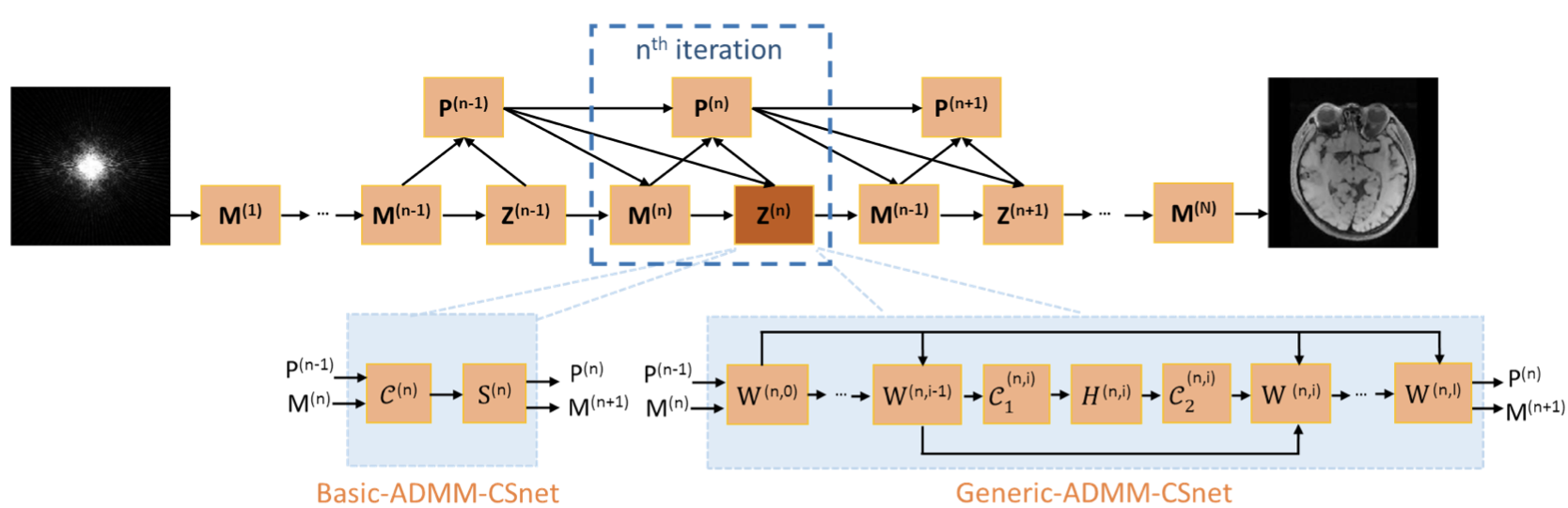
basic-ADMM-CSNet: learns the regularization parameters in the ADMM algorithm
(Deep ADMM-Net for Compressive Sensing MRI) (read code)
\[min\quad \frac{1}{2}||Am-f||_2^2+\sum _l\lambda_lg(\mathbf{z_l})+\sum_l<\mathbf{\beta_l,D_lm-z_l}>+\sum_l\frac{\rho_l}{2}||\mathbf{z_l-D_lm}||_2^2\]augmented Lagrangian function: 最后一项是penalty
< = >
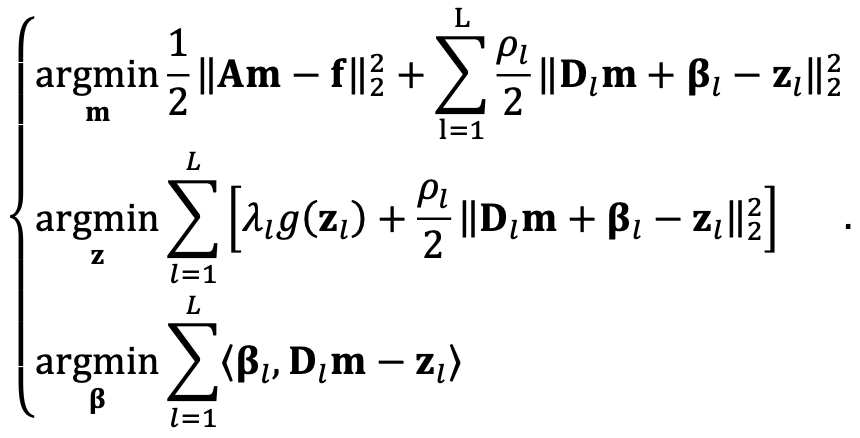
求得
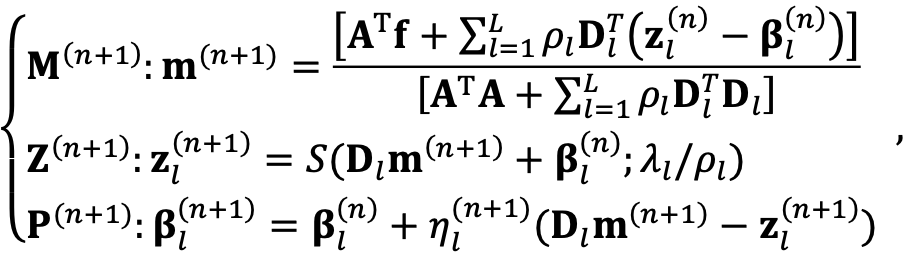
Generic-ADMM-CSNet: learns the image transformations and nonlinear operators used for the regularization function
(ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing)
区别在于$\mathbf{z={z_1,z_2,…,z_l}}$是在spatial domain,因此$\mathbf{D_lz}$ is sparse
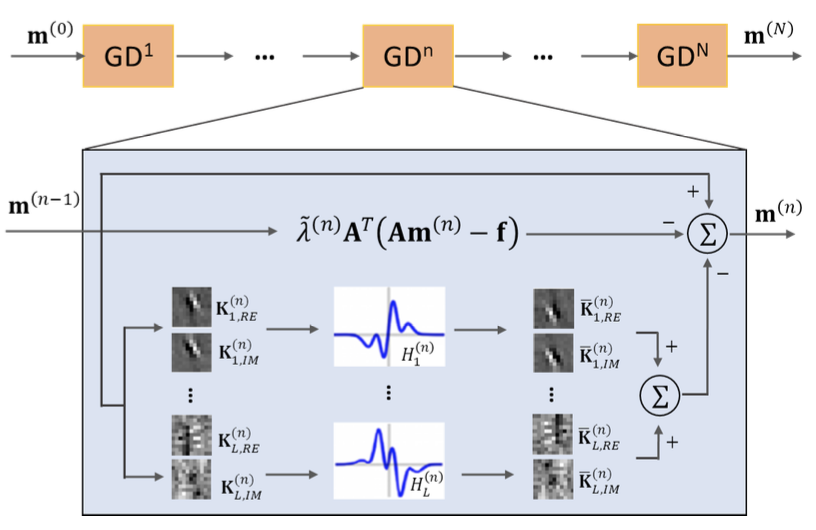
2) Variational-net (multi-coil)
(Learning a variational network for reconstruction of accelerated MRI data) (read code)
$G(\mathbf{m})=\sum_l<g_l(\mathbf{D_lm}),1>$
其中$D_l$表示convolution with kernel $\mathbf{K_l}$ (learnable params)
$H_l^{(n)}$是activation function(learnable params)
$\lambda^{(n)}$ (learnable params)
$A$由sub-Nyquist Fourier encoding和sensitivity encoding 构成
3) ISTA-net (iterative shrinkage-thresholding algorithm)
(ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing)
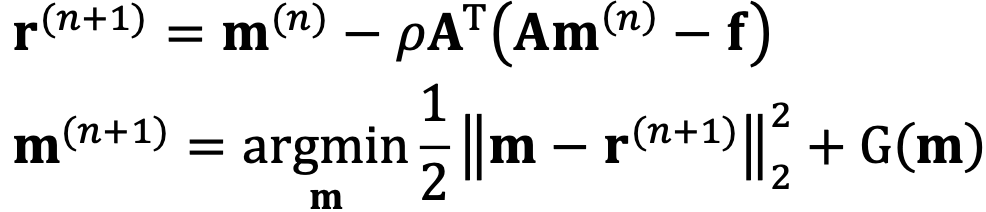
传统的ISTA算法
其中$G(\mathbf{m})=\lambda||\mathbf{Dm}||_1$,$\rho$是step size
传统ISTA算法缺点是当$\mathbf{D}$是non-orthogonal, non-linear的时候,很难算出$\mathbf{m}^{(n+1)}$
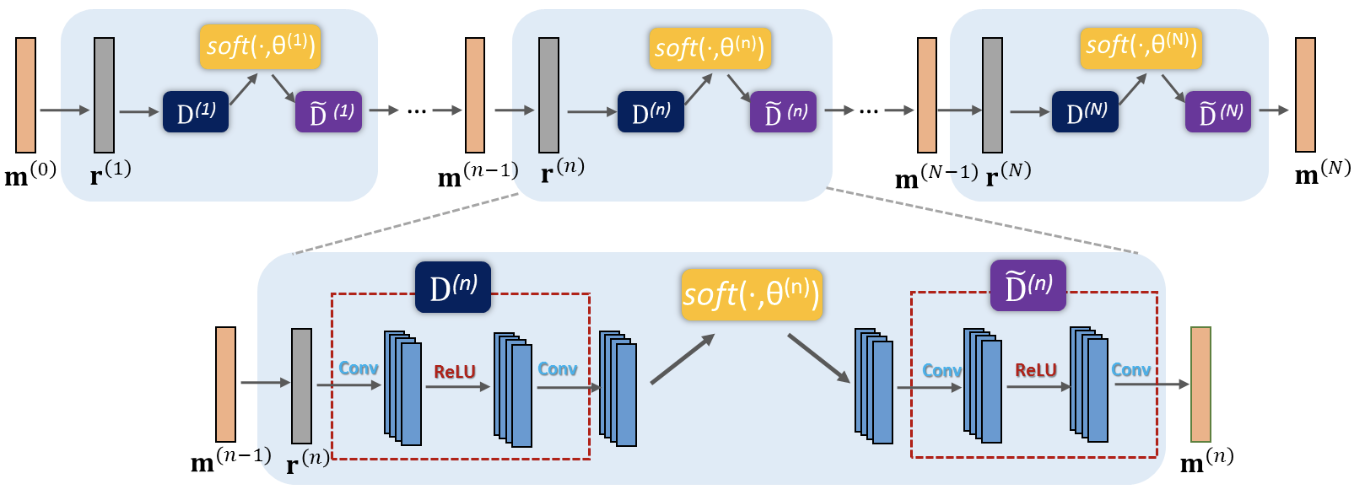
ISTA-net
ISTA net 将ISTA的优化目标改成了如下形式
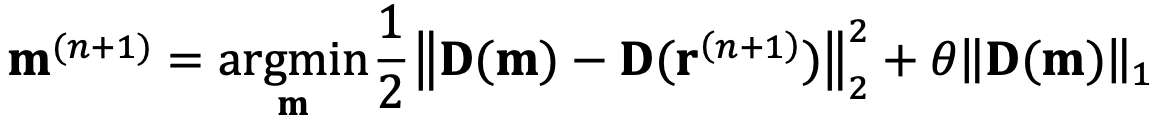
进而获得解如下?
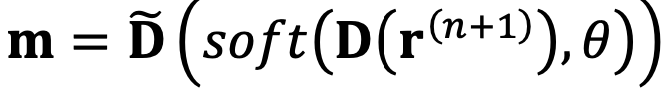
Data-driven deep learning for fast MR
aliased image → clean image (Accelerating Magnetic Resonance Imaging via Deep Learning)
1) Basic data-driven network for MR reconstruction
AUTOMAP: k-space data → 1 layer fully-connected network → reconstructed image
RAKI: 3 layer CNN for k-space interpolation (parallel imaging)
GAN: correct aliasing artifacts from undersampled data
(Compressed Sensing MRI Reconstruction Using a Generative Adversarial Network With a Cyclic Loss)
(Deep Generative Adversarial Neural Networks for Compressive Sensing MRI)
QSMnet: 3D U-Net → QSM from single orientation data
DRONE: 4-layer MLP → tissue properties and predict T1 and T2 from 2D MRF data.
2) Domain knowledge from MRI
- Fourier transform
-
Regularization term
2 options to integrate network and CS
read (Accelerating Magnetic Resonance Imaging via Deep Learning)
- use the image reconstructed from the trained network as initialization for CS
- use the image generated by network as reference image in additional regularization
-
Data consistency
consistency between data in image space and k-space
- KIKI-net

- spatio-temporal correlations
- residual U-net
- convolutional RNN
- Quantitative parameters
Integrated deep learning for fast MR
特点
- It is an unrolling version of optimization algorithm
- at least one sub-problem is solved using data-driven “black box”
1) Connection between two approaches
2) Integrated approaches for MR reconstruction
- MoDL
MoDL: Model-Based Deep Learning Architecture for Inverse Problems
\[\mathbf{m}^{(n+1)}=argmin||\mathbf{Am-f}||_2^2+\lambda||\mathbf{m-z^{(n)}}||^2_2\] \[\mathbf{z}^{(n+1)}=C(\mathbf{m}^{(n+1)})\]
regularization term: 降噪后的和降噪前的图像的差别是稀疏的
- DCCNN
A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction
- PD-net
Learning Primal Dual Network for Fast MR Imaging
unrolling version of the primal dual algorithm
\[min\quad F(\mathbf{Am})+G(\mathbf{m)}\] \[\left\{\begin{aligned} d_{n+1}&=C_1(d_n,Am_n,f)\\ m_{n+1}&=C_2(m_n,A^{*}d_{n+1})\\ \end{aligned}\right.\]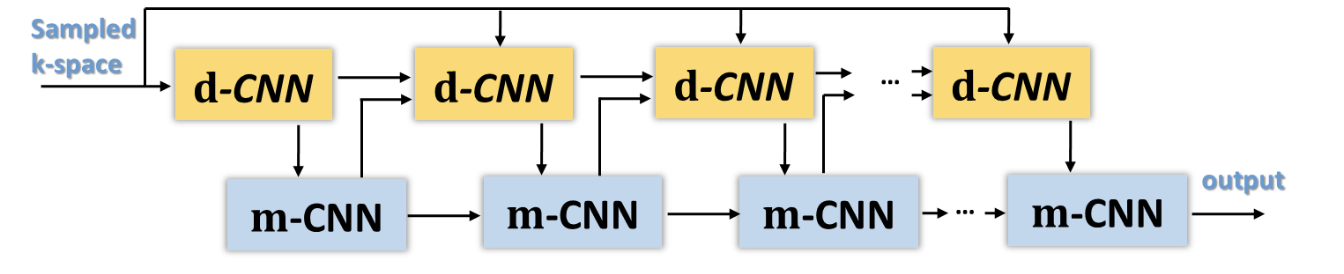
Some signal processing issues
1) Theoretical analysis
framelet
2) Transfer learning
-
contrast, SNR, image content difference between training & testing data
→ noise + slightly blurred images with residual artifacts
- network trained on regular undersampled data can be generalized to randomly undersampled data
-
AUTOMAP: train on natural images → apply to MRI images
Image reconstruction by domain-transform manifold learning
3) Relationship with other learning-based approaches
-
compressed sensing with dictionary learning
linear transform learned using simulated data from theoretical model/ low-res image
MR image reconstruction from highly undersampled k-space data by dictionary learning
Adaptive Dictionary Learning in Sparse Gradient Domain for Image Recovery
-
compressed sensing with manifold learning
nonlinear prior of low-dim manifold is learned from training data
4) Other issues in deep learning approaches
separate the real & imaginary / magnitude & phase parts into two channels
To handle multi-coil data:
- convey the pre-calculated coil sensitivity into the network
- reconstruct the image from the multi-channel data through network
- learns the k-space interpolation from ACS data
Non-cartesian reconstruction
- AUTOMAP: reconstruct directly from non-Cartesian samples
- domain adaptation from CT projection
Deep learning with domain adaptation for accelerated projection-reconstruction MR
5) Future Directions
Deep learning to integrate reconstruction & diagnostic