Chapter 1, Introduction

Diffusion 原理，Free Diffusion

Fick’s first law:

\[J=-D\nabla C\]

J是net particle flux，C是particle concentration，D is diffusion coefficient (defined by size of diffusion molecules, temperature， microstructural features of the environment)

diffusion 来源：仅仅是 collisions between atoms or molecules。不管在平衡态还是非平衡态，微观上都有运动。

\[<x^2>=2D\Delta\]

x 是diffusion distance，时间是$\Delta$。

MR signal attenuation，用来测量MR的relaxation。

\[E(q)=S(q)/S(0), \quad q=\gamma \delta G\]

eliminates the effect of relaxation。

\[E(q)=\int\rho(x_1)\int P(x_1,x_2,\Delta)e^{-iq(x_2-x_1)}dx_1dx_2\]

Diffusion propogator (Green’s function): $P(x_1,x_2,\Delta)$，表示particle 一开始在$x_1$，$\Delta$之后，在$x_2$的概率。

$\rho(x_1)$：代表了在$x_1$处找到一个particle 的概率。

\[lim_{t->\infin}P(x_1,x_2,t)=\rho(x_1)\]

因为当 $t->\infin$时，一个particle到空间任何一个位置都有相同的概率，这种情况就跟在$x_1$处有一个particle 一样。

Free Diffusion：$E(q)=e^{-q^2D\Delta}$， 考虑pulse duration后，$E(q)=e^{-q^2D\Delta-\delta/3}=e^{-bD}$，

b-value：其中的$b=q^2(\Delta-\delta/3)$

上述方法可以用来描述free, anisotropic diffusion in the principal frame of reference

我们不希望预设任何数学模型，只希望获得local propogator来measure microstructural features。但是low resolution和inability to obtain spin density阻碍了local propogator的获得，因此我们ensemble average来简化问题。

\[E(q)=\int\overline{P}(x,\Delta)e^{-iqx}dx\\\overline{P}(x,\Delta)=\int\rho(x_1)P(x_1,x_1+\Delta x,t)dx_1\]

可以看到$E(q)$和$x$之间通过 Fourier Transform联系起来，q-space imaging, Diffusion Spectrum Imaging。

Diffusion in Neural Tissue (影响free diffusion 的因素)

Chapter 2, Pulse Sequence for Diffusion-Weighted MRI

Adding Diffusion Weighting to Pulse Sequence

generalized b-value definition: $b=\int |k_x(t)|^2+|k_y(t)|^2+|k_z(t)|^2 dt$，$k_x(t)=\gamma\int G_x(t)dt$ position on k-space

Two sources of error in DWI: eddy currents, gradient nonlinearity

eddy currents 原理：gradient coils 会产生magnetic fields ，进而在超导线圈周围的液氦中产生感生电场，也就是eddy current。主要由gradient slewing 产生，梯形gradient的上升支和下降支可以相互抵消。

Bulk Motion Sensitivity

Two sources of bulk motion: head movement,cardiac pulsation

different shots will lead to different motion, so DWI are generally limited to single-shot, and the motion remains constant.

一般为了减少采集时间，默认为中心对称的k-space上，我们会进行asymmetric sampling，其中一半可以减少采样数。但是如果由于head rotation，对称假设不再满足，进而产生artifact

navigator correction

Single-shot EPI (SS-EPI)

  • geometric warping from field inhomogeneities
  • geometric warping from gradient-induced eddy currents
  • Intra-voxel dephasing effects on image resolution

Chapter 3, Diffusion Acquisition: Pushing the Boundaries

Chapter 4, Geometric Distortions in Diffusion MRI

dMRI 图像相比与structural image 模糊的原因主要由acquisition 序列EPI造成

EPI对 off-resonance field (实际的field 和我们想要的field的差别)比较敏感。

dMRI中的off-resonance field 由 head 和 after effects of switching the gradients 造成

Why are EPI distorted

EPI distortion 一般沿着PE方向。

FE gradient: 500~1000Hz/mm

inhomogeneity: <100Hz

所以在FE direction，误差大概在0.1~0.2 mm

但是在PE方向上，因为EPI上的PE gradient是“blip”

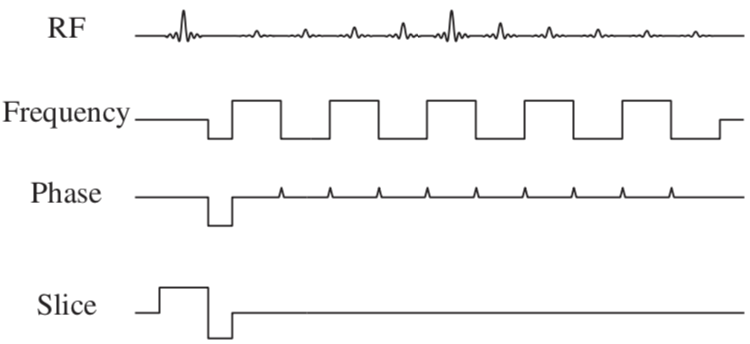
所以$T_D$时间内，在一个voxel 的长度$S$上要形成$2\pi/N_{PE}$的phase difference。也就是PE gradient是

$1/N_{PE}T_DS$ Hz/mm。其中$T_D=5\times10^{-4}s$，$S=2mm$，$N_{PE}=96$，PE gradient是10Hz/mm。因此在PE direction上，误差大概是10mm。

一般PE direction是沿着大脑的左右方向，因为大脑的宽度小于长度。

Where does the off-resonance field come from

  1. Susceptibility-Induced Field
    1. Frequency Calibration and Shimming
      • 常数项的场偏移首先会被消除。e.g., 想要3T场强，3T左右的场都会被尝试一遍，直到找到最佳的场强。
      • pre-scan时会采集low-resolution image，然后使用shim coil去抵消一部分off-resonance field，剩下的uncompensated part就是我们指的”off-resonance field”
    2. Subject Movement

  2. Eddy Current-Induced Field

    fields are some linear combination of linear gradients in the x-, y-, and z-directions (Jezzard et al., 1998)

    expected distortions are y-zoom, yx- and yz-shear for data acquired with PE in the y-direction, x-zoom, xy- and xz-shear for PE along x.

  3. Concomitant Fields

Modified Imaging Techniques that Yield Less-Distorted Images

  1. Parallel Imaging

  2. Sequences to Reduce Eddy Currents

Imaging Techniques that Acquire Information about the Off-Resonance Field

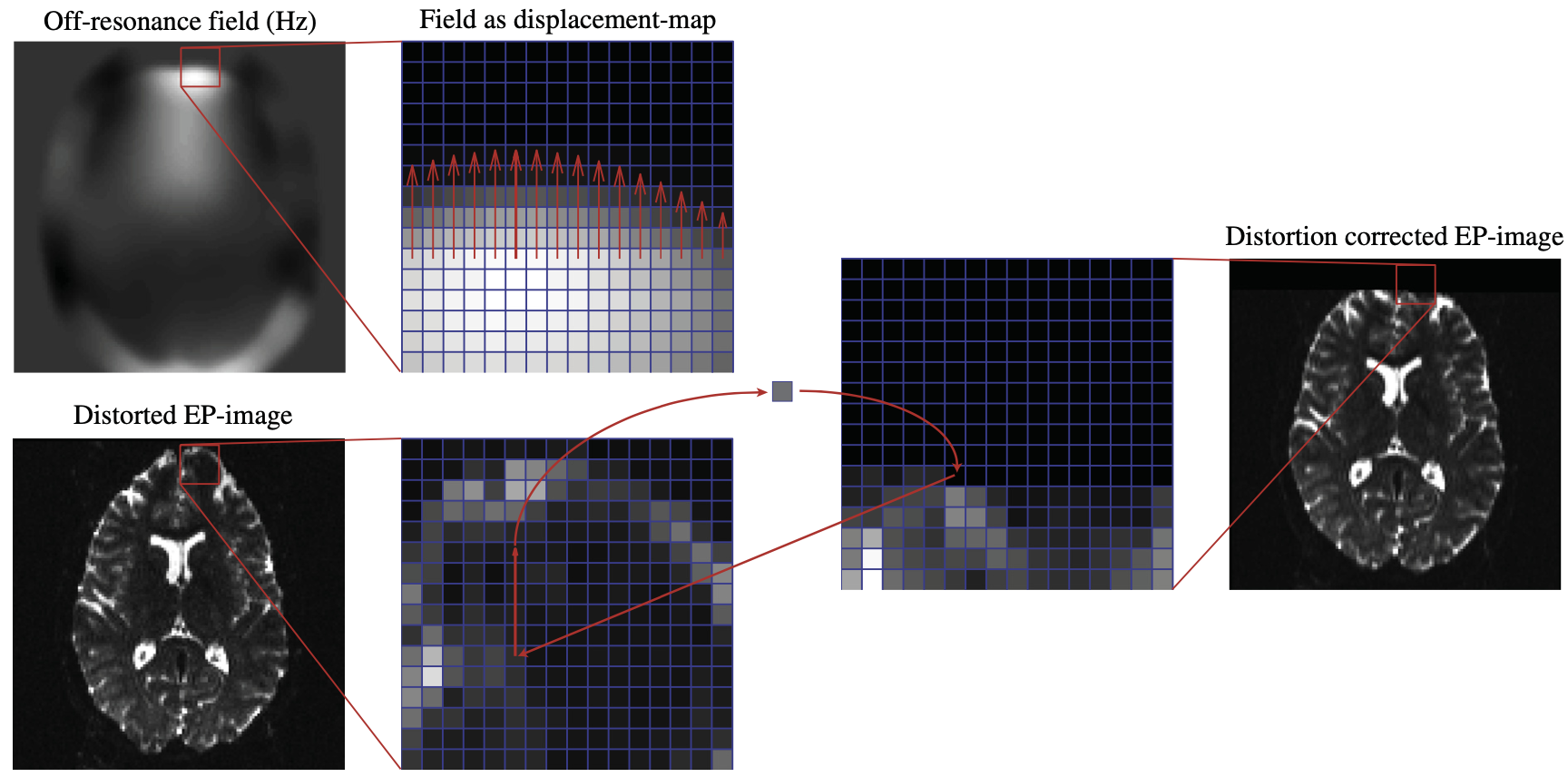
  1. Unwarping an Image when the Off-Resonance Field is Known

    如果off-resonance field 和 acquisition parameters 知道，那么就可以从distorted image 重建出corrected image。

  2. Fieldmaps

  3. How to Choose $\Delta TE$ for your Fieldmaps

Image Registration-Based Methods for Correcting Distortions

Recent Work at the FMRIB

Chapter 5, Gaussian Modeling of the Diffusion Signal

Chapter 6, Multiple Fibers: Beyond the Diffusion Tensor