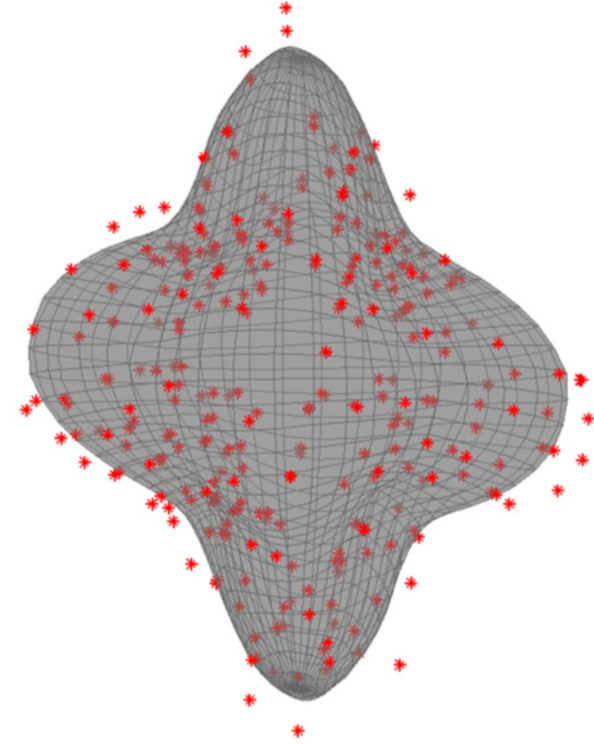
Non-parametric representation and prediction of single- and multi-shell diffusion-weighted MRI data using Gaussian processes

目的：dMRI有image distortion, signal loss, 等问题。为了校正这些问题，需要预测正确的dMRI图像应该是怎么样的。

Geostatistics: a class of statics that analyze and predict spatial/ spatiotemporal relationship

diffusion signal 在q-ball 上的性质

• The signal changes smoothly as the angle of the diffusion weighting direction changes.
• The signal is axially symmetric, i.e.the signal along g is identical to the signal along − g.

covariance function

covariance function 的来源：通过sample 一些图像，计算互相之间的covariance function，以对应角度差$\theta$作为自变量，画出函数图像，然后看看与怎样的convariance function 拟合的比较好。

1. exponential model: $C(\theta)=e^{-\theta/a},\theta \in [0,\pi]$
2. spherical model:

$\theta(\vec{g},\vec{g’})=arccos|<\vec{g},\vec{g’}>|$ （轴对称的性质）

Single-shell data

Optimize hyperparameters

marginal likelihood maximization: $log(p(\mathbf{y}|\beta,M))=-\frac{1}{2} \mathbf{y^TK_y^{-1}y}-\frac{1}{2}log|\mathbf{K_y}|+c$

$\mathbf{y}$是这个voxel上所有g 方向的signal 组成的向量。在所有的voxel $\mathbf{y}$上对上式求和。

其中$\beta$表示所有的hyperparameter，M表示选择的covariance function。

其中$K_y$是带有噪声项的covariance matrix。$K_y=K+\sigma^2I$

*用Laplace approximation来在两个covariance function中进行选择PRML中的6.4.6。（不是特别重要，GP 的预测效果和具体的covariance function 的具体形式关系不大）

用leave-one-out 尤其是cross validation的方法来检查hyperparameter估计效果

Multi-shell data

covariance function: $k(\mathbf{x,x’})=C_{\theta}C_b$，其中$C_{b}=exp(-\frac{(logb-logb’)^2}{2l^2})$。

两个b-value时的例子：

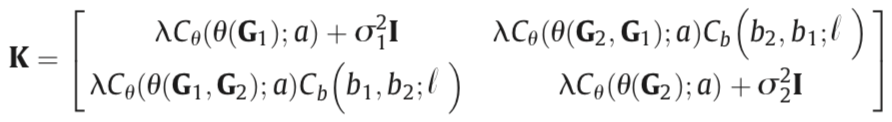
Optimization

梯度优化，PRML中的

启发式，本文中的Nelder–Mead simplex method

Results

这幅图表示的是一个voxel。三维图像上每个点的角度表示diffusion的角度，极径表示diffusitivity。红色的点表示测量值，灰色面表示GP prediction。