1D case

equally spaced samples $x_n$ ———→ nonuniform spaced frequency locations ${\omega_m}$

FT: $X(\omega)=\sum_{n=0}^{N-1}x_ne^{-i\omega n}$

直接计算需要$O(MN)$，快速的计算方法就是 NUFFT

1. Weighted K-point FFT ( K≥N )

$Y_k =\sum_{n=0}^{N-1}s_nx_ne^{-i\gamma kn}$， (k= 0, …, K-1； $\gamma=2\pi/K$)

其中$s_n$是scaling vector，partially pre-compensate for imperfections in the subsequent frequency-domain interpolation

2. Approximate $X(\omega _m)$ by interpolating $Y_k$

$\hat{X}(\omega_m)=\sum_{k=0}^{K-1}v_{mk}^{*}Y_k$，(m=1,…., M)

傅立叶反变换$Y_k$，有$x_n=1/K\sum_{k=0}^{K-1}Y_ke^{i\gamma kn}$

根据FT，$X(\omega)=\sum_{n=0}^{N-1}x_ne^{-i\omega n}=X(\omega)=\sum_{n=0}^{N-1}\left[\frac{1}{K}\sum_{k=0}^{K-1}Y_ke^{i\gamma kn}\right]e^{-i\omega n}=\sum_{k=0}^{K-1}Y_k\left[\sum_{n=0}^{N-1}\frac{1}{K}e^{in(\gamma k-\omega)}\right]$

Dirichlet-like “periodic sinc” function

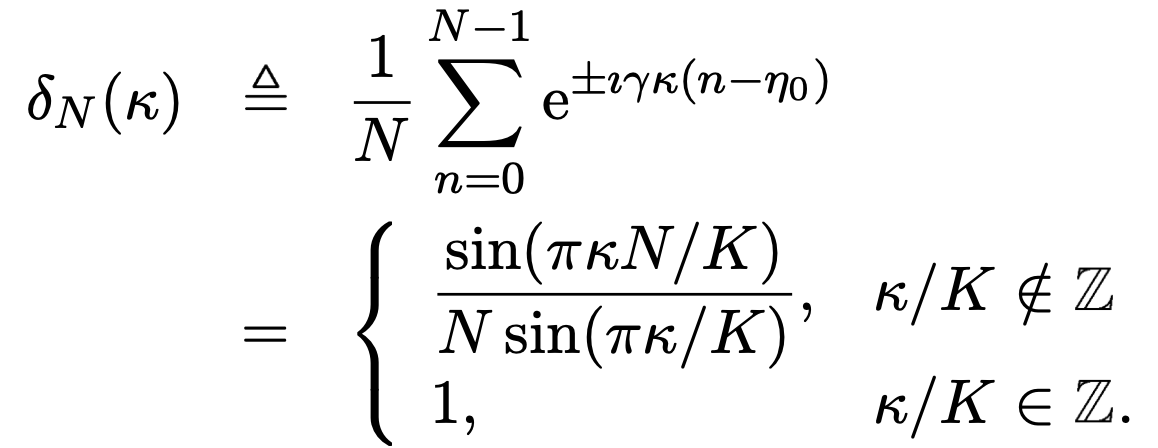
现在复杂度为$O(MK)$，依旧很高

为了进一步降低计算复杂度，我们仅选择与$\omega_m$最近的 j 个$Y_k$进行interpolation。因此计算复杂度为$O(MJ),J\ll K$。

定义integer offset $k_m=k_0(\omega_m)$，定义为离$\omega _m$的最大offset （也就是 $J$个$Y_k$中最小的一个）

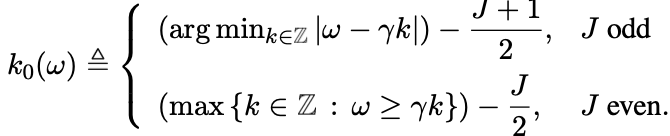
定义$**u_j(\omega _m), j=1,…J$，为$J$个interpolation weights**。

$\hat{X}(\omega_m)=\sum_{j=1}^{J}Y_{k_m+j}u^*_j(\omega _m)$

下一步就是选择$u_j(\omega _m)$，使得$\hat{X}(\omega _m)$接近$X(\omega _m)$

3. Min-max criterion for choosing $u_j(\omega _m)$

$x$是任意的N维signal（已经归一化），因此对 $s$ 和 $u$ 的优化分别由两个 $min,max$ 构成。

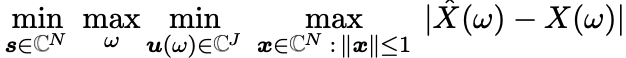
对于外层的$min, max$，仅有数值优化解，对于内层的$min,max$，有解析解

  • 对于内层的 $min,max$

    $|\hat{X}(\omega _m)-X(\omega _m)|=|\sum_{j=1}^{J}Y_{k_m+j}u^*_j(\omega _m)-X(\omega _m)|$

    带入$Y_k$

    先计算$\mathop{max}\limits_{||x||=1}$

    $\sum_{j=1}^{J}u^*_j(\omega _m)\left[\sum_{n=0}^{N-1}s_nx_ne^{-i\gamma (k_m+j)n}\right]-\sum_{n=0}^{N-1}x_ne^{-i\omega n}$

    =$\sqrt{N}\sum_{n=0}^{N-1}x_n\cdot\frac{1}{\sqrt{N}}\left[s_n\sum_{j=1}^{J}u_j^*(\omega_m)e^{-i\gamma(k_0(\omega)+j)n}-e^{-i\omega_mn}\right]$

    =$\sqrt{N}<\vec{x},\vec{g}(\omega_m)>$

    $\mathop{max}\limits_{||x||=1}=||g(\omega)||_2^2$，当$\vec{x}$与$\vec{g}(\omega_m)$共线。

    进而求 $\mathop{min}\limits_{u}$

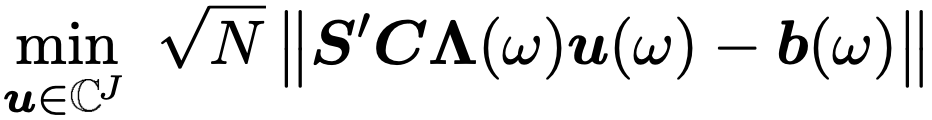
    当$S’C\Lambda u=b$，即 $u=\Lambda’[C’SS’C]^{-1}C’Sb$ 时，最小。

    • 通过对$S’C=QR$ 分解，进而$u=\Lambda’(\omega)R^{-1}Q’b(\omega)$，同时QR分解与 $x$ 无关，可以提前计算。

4. Efficient computation

将上述式子重新写成 $u(\omega)=\Lambda’(\omega)Tr(\omega)$，( $T=[C’SS’C]^{-1}$，$r’(\omega)=C’Sb(\omega)$ )

  • T是可以提前计算的，为了快速计算T，将$s_n$写成 truncated fourier series

    $s_n=\sum_{t=-L}^L \alpha_te^{i\gamma\beta t(n-\mu_0)}$

    $T^{-1}_{l,j}=\sum_{n=0}^{N-1}C^*_{nl}S_nS_n^*C_{nj}$

    $=1/N\sum_{n=0}^{N-1}\sum_{t=-L}^{L}\sum_{s=-L}^{L}\alpha_t\alpha_s^*e^{i\gamma(j-l+\beta(t-s))(n-\mu_0)}$

    $=\sum_{t=-L}^{L}\sum_{s=-L}^{L}\alpha_t\alpha_s^* \delta_N(j-l+\beta(t-s))$

    因此$T$ 既是 $Hermitian$ 也是 $Toeplitz$ 。

    • $Hermitian$ : 共轭对称矩阵 ( $**l$ 和 $j$ 可以对换** )
    • $Toeplitz$ : 矩阵各斜线上元素相等 ( 只和 $j-l$ 有关 )

  • $r’(\omega)=C’Sb(\omega)$

    $r_j(\omega)=\sum_{t=-L}^{L}\alpha_t \frac{1}{N}\sum_{n=0}^{N-1}e^{i\gamma[\omega/\gamma-k_0(\omega)-j+\beta t](n-\mu_0)}$

    $=\sum_{t=-L}^{L}\alpha_t \delta_N(\omega/\gamma-k_0(\omega)-j+\beta t)$

综上，可以提前计算 $T$ ,并且 $T$ 只有$J\times J$ 比较小

5. 减少提前计算项对N的依赖

现在计算$T,r$ 都依赖于 $\delta_N$。也就是换一个signal length N，就要重新计算一次。

现在希望只依赖于$\mu=K/N$。当K 很大时$\delta_N(t)\approx sinc(t/\mu)$，其中$sinc(t)=sin(\pi t)/\pi t$。

6. Multidimensional NUFFT

$\tilde{T}_{2D}=\tilde{T}_{1D}(J_1,\mu_1)\otimes\tilde{T}_{1D}(J_2,\mu_2)$

$\tilde{r}_{2D}=\tilde{r}_{1D}(J_1,\mu_1)\otimes\tilde{r}_{1D}(J_2,\mu_2)$

7. Reduced FFT

当$K/N=integer$时，根据 k%(K/N) 余数分组， 可以分 K/N 个FFT 计算 复杂度为 $O(K/N \cdot Nlog(N))$

8. Adjoint operator

用于iterative algorithm中的

首先有$\hat{X}=Gx$，$G=VWS$，其中$V$就是interpolation weights, $W_{kn}=e^{-i\gamma kn}$是DFT matrix, $S$ 跟之前的相同。

现在要计算$G’\tilde{y}=S’W’V’\tilde{y}$，由于$G’$ 太大，不能直接矩阵乘法

  • 先计算$\tilde{X}_k=\sum_{m=1}^M v_{mk}\tilde{y}_m$
  • 再计算$\tilde{x}_n=\sum_{k=0}^{K-1}\tilde{X}_ke^{i\gamma kn}$

9. Nonuniform inverse FFT

uniformly spaced frequency samples → nonuniform spatial locations

10. Inverse NUFFT

e.g., non-Cartesian k-space → MRI recon

\[\hat{x}=\mathop{argmin}\limits_{x}||X-Gx||\]

$G$ is adjoint operator。

只能使用iterative algorithm求解，而iterative algorithm 经常需要 forward calculation object space→ frequency space ，这时就是NUFFT有用的时候了。

11. 选择$s_n$

12. 传统插值方法

  • Apodized Dirichlet

  • Truncated Gaussian bell

  • Kaiser Bessel