Regularization based reconstruction of asymmetric susceptibility tensor

Github Repo

Purpose:

Susceptibility tensor imaging has attracted increasing amounts of attention for its potential of achieving ultra high resolution. Comparing to the diffusion tensor imaging, which has reached a stage where we have to choose between high resolution and short scanning time, susceptibility tensor imaging can easily achieve submillimeter resolution and allow researchers to probe more sophisticated in-vivo microstructures. Nevertheless, there are a few obstacles of in susceptibility tensor imaging that urges to overcome before this technique can be applied to clinical study.

Firstly, the existed methods for susceptibility tensor reconstruction are not accurate enough to reveal the susceptibility tensor distribution. Part of the problem may arise from the inaccurate calculation to inverse the phase perturbation. The 3 dimensional magnetic resonance images normally consist of more than $10^6$ voxels which challenges the computation and storage capability of computers. More importantly, the inversion matrix is highly sparse as a portion of regions possess isotropic susceptibility or no susceptibility sources. A common approach dealing with this problem is to transform the inverse calculation problem to a minimization problem which forces the forward calculation with the estimated susceptibility to be similar to the detected phase distribution. A least-square method will be applied to iteratively solve the minimization problem. The methods used to reconstruct the susceptibility tensor are similar as those developed for quantitative susceptibility mapping. More constraints are introduced into the iterative methods as regularization terms in quantitative susceptibility mapping. However, as far as I understand, few constraints has ever been applied to susceptibility tensor imaging. Therefore, we propose to integrate the prior information into the reconstruction process. To be more specific, the morphology based binary mask will be used to impose constraints on the rank-2 tensor in regions where susceptibility is regarded as isotropic. Such constraints add to the robustness of the inverse calculation.

Another obstacle lies in the imperfect relationship between the phase map, susceptibility tensor and the fiber orientations. The existed reconstruction methods tend to model the relationship between the phase map and the susceptibility tensor is purely dominated by the convolution of a dipole kernel. Researchers also assumed the principle eigenvector of the susceptibility tensor to be the orientation of the white matter fibers. Such assumption tried to transfer the models in diffusion tensor imaging to susceptibility tensor imaging without complete and solid biophysical foundations. Though previous research about rat brain has partially proved the effectiveness of the susceptibility tensor imaging in tracking fibers, the predictions in human brain sometimes contradicts the actual fiber orientations. Despite the significance of finding more accurate biophysical underpinnings for the susceptibility tensor, in this study, we focus on the improving the relationship between phase map and the susceptibility tensor. Our improvements based on two assumptions. Firstly, the symmetric property of the rank-2 tensor does not hold as images will inevitably be contaminated by noise accumulated during acquisition and pre-processing. Secondly, the intrinsic properties of tissue like chemical shift/ exchange will also contribute to the phase map as a constant offset.

In order to test the improved inverse relationship, we propose to jointly reconstruct the constant offset and the anisotropic susceptibility tensor, the morphology based binary mask will also be integrated as additional constraints.

Methods:

Our methods were tested using numerical simulations. A simple customized 3D phantom based on the Shepp-Logan one were first constructed. A set of nine orientations were manually designed with maximum rotation of $60^{\circ}$. Phase perturbations under different orientations were calculated using the model that relates the susceptibility tensor and phase. To validate the effectiveness of our method in suppressing the noise in the phase map, Gaussian noise was added to the phase map with SNR of 30. In addition, constant offset was set for each region respectively and added to each phase map. The morphology based binary mask representing the isotropic regions was derived from phantom directly.

The susceptibility tensor and constant offset was then jointly estimated using LSQR. The hyper parameters including the tolerance of LSQR and weight for regularization terms were decided based on a number of trials.

To further validate the effectiveness, we adopted a numerical model based one diffusion tensor imaging. In order to make the model aligns with our assumptions, we modified it by setting the non-diagonal elements to zero in isotropic regions. The binary mask was obtained by segmenting the corresponding T1 image using FSL.

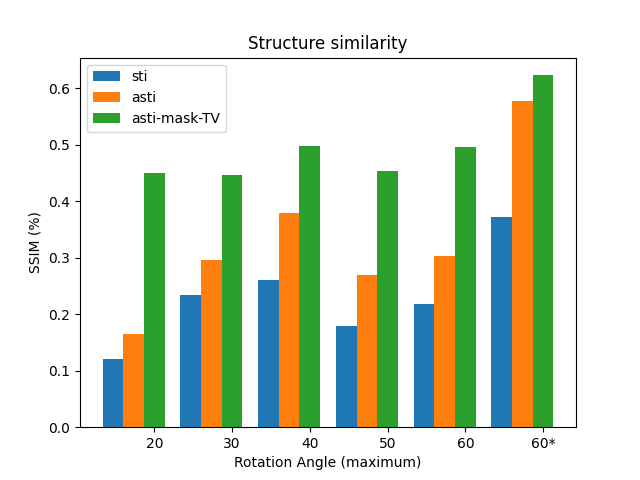
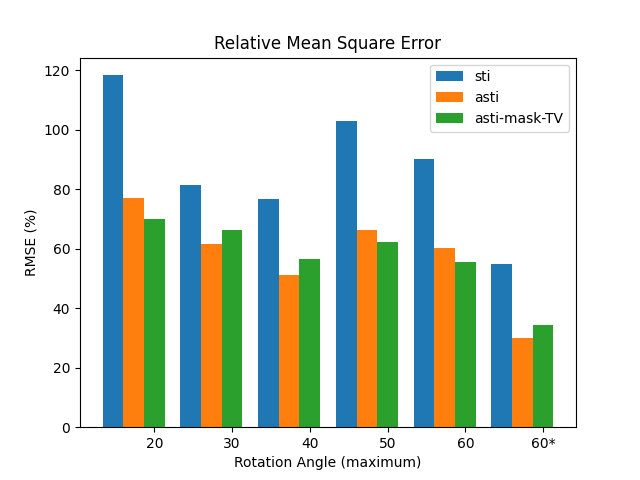
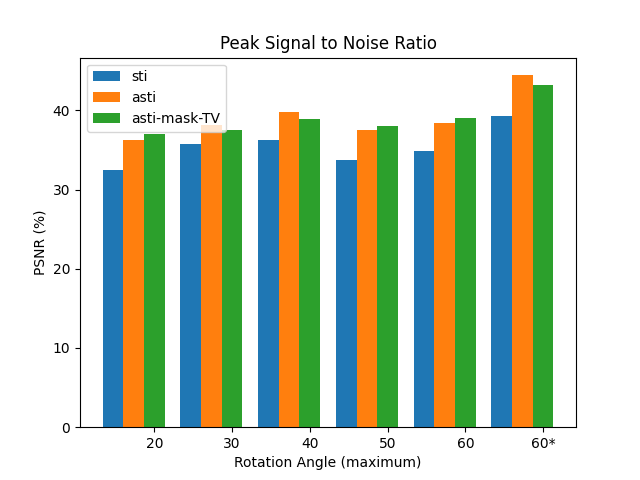
We take a step further comparing to the experiments conducted on the previous simple phantom. Six sets of orientations were generated, five out of which were randomly picked with maximum rotation angles ranging from $20^{\circ}$~$60^{\circ}$. The last set of orientations were equally distributed in space. Three different reconstruction approaches, including the conventional methods, the anisotropic tensor one and ours, were tested on all six sets. The experiments were designed to demonstrate the advantage of our methods.

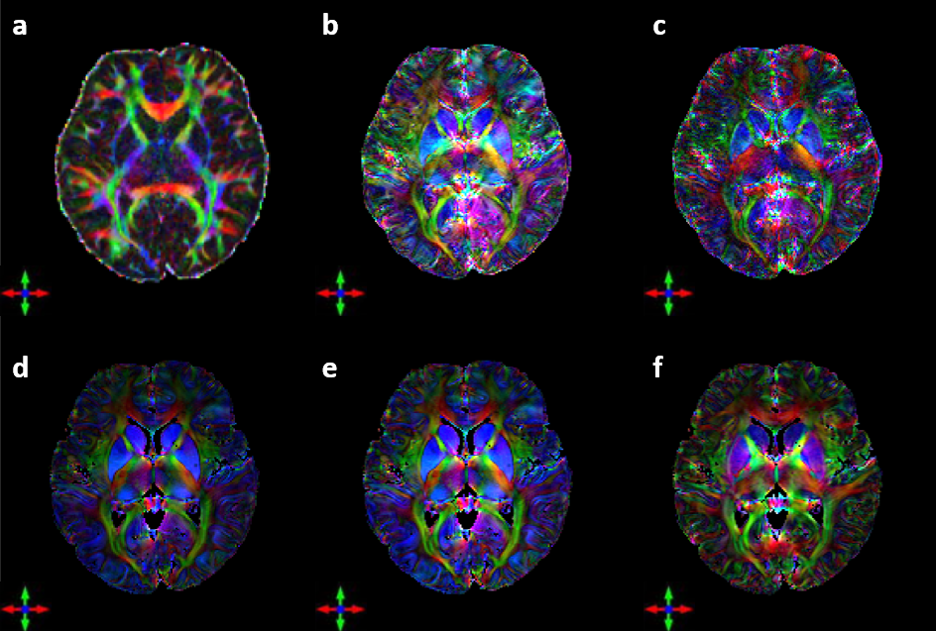
After the validations of the above two phantoms, we applied our methods to the in-vivo data with 17 different orientations. We applied our methods to jointly estimate the susceptibility tensor and constant offset. The binary mask from the segmentation of the corresponding magnitude image was used to impose the isotropic constraint on cerebral spinal fluid region. A diffusion tensor image was generated and registered to our susceptibility map using FSL for comparison.

Results:

In the part of numerical simulation, we verified the accuracy of our methods using two different phantoms. Comparing the results in the simplest phantom, artifacts can be observed in isotropic regions in magnetic susceptibility anisotropy images calculated by the conventional methods. In addition, large amounts of noise existed in the final result. Our methods, however, produced the perfect result with high SNR and consistency with the phantom. In the more realistic model based on diffusion tensor imaging, our method performed constantly superior to the conventional one.

In the experiments that compares the performance of different methods under different orientations, we also observed that our method beated the conventional one. One useful discovery is that the reconstruction of asymmetirc tensor gave better results than that of symmetric tensor. Considering about 150\% increase in the number of unknown elements when solving the asymmetirc one, the results proved the negative effect of noise on the susceptibility tensor.

Another important discovery arises from comparing the results of two different sampling strategies. The results calculated from the equally spaced orientations and the randomly picked one demonstrated the significance in the choice of orientations. In susceptibility tensor imaging, one of the most troubling problem is rotating the subject during acquisition. Therefore, a common principle to follow is having minimal rotation angles and times. Now that we have discovered the significance in the distribution of orientations, given maximum angles and times, we can further develop a strategy as guidance for optimal orientations during acquisition.

Unlike numerical simulation, we do not have knowledge of noise distribution on the phase map. From the final results, however, we can easily notice the noise suppression effect of our methods, which further proved the asymmetric reconstruction applies to more general noise accumulated before reconstruction. One astonishing discovery is the important effect of constant offset. Comparing the the results produce by purely asymmetric tensor reconstruction and additional consideration of constant offset, the peripheral regions of the brain were dominated by purple, showing unified direction, which should not appear in isotropic regions. In fact, the result obtained by the method considering the constant offset seems more realistic as it shows no obvious directions. The magnetic susceptibility anisotropy also has lower gray values.

Although previous studies have shown that the susceptibility tensor can also be used to study the orientation of white matter fibers, some differences exist between the susceptibility tensor and the diffusion tensor. On the one hand, these differences may be caused by the different physical principles of the two imaging methods. On the other hand, it reflects the limitations of susceptibility imaging. Although magnetic susceptibility tensor imaging possesses the inherent advantage of high resolution, the principal eigenvector of magnetic susceptibility tensor sometimes disagrees with the actual orientations of fibers. Therefore, how to better model the relationship of the magnetic susceptibility tensor with the direction of fibers can be critical before the novel technique can be transferred to clinical applications.

Conclusion:

In conclusion, the results of numerical simulation prove the effectiveness of methods in increasing both the SNR and accuracy. The results calculated from the in-vivo data demonstrated the significant improvements of our method comparing to the conventional one in terms of describing the fiber orientations.